Poincaires Welt hätte vier Dimensionen

Paul schaut nachdenklich in die Ferne.
Vasco hatte ihm immer noch keine Antwort darauf gegeben, ob er sich nun hinter Einsteins Metrik etwas vorstellen darf oder nicht. Andererseits war diese Antwort gar nicht mehr wichtig. Paul ist auch so klar geworden, daß unterschiedliche Vorstellungen vom Raum zu Mißverständnissen führen müssen. Er wird nicht mehr an Einsteins Raum mit Metrik herummäkeln - das nimmt er sich zumindest vor. Dieser leere Raum mit Struktur, der ist ihm aber einfach zu abstrakt, zu schwer vorstellbar.
Paul liegt an Gedankenexperimenten und deshalb beabsichtigt er auch weiterhin seine Umgebung mit Jonas´ Augen zu betrachten.
Doch in einem Punkt - dessen wird er sich mehr und mehr bewußt - ist die Allgemeine Relativitätstheorie gegenüber Jonas eindeutig im Vorteil:
Sie hat Dimensionen!
Sie hat genau die Dimensionen, die Paul in Jonas´ Welt noch nicht einmal von Weitem erkennen kann.
„Die Dimensionen,“ sagt er leise, „Die Dimensionen, Vasco. Die räumlichen Dimensionen wie Länge, Breite Höhe - sie hängen doch untrennbar mit dem Raum zusammen, nicht wahr?“
„Das sollte man denken.“ weicht Vasco aus. „In welcher Beziehung sollten denn nach deiner Auffassung die Dimensionen und der Raum stehen? Was verlangst du von den Dimensionen?“
„Sie sollen mir als geeignete Maßstäbe dienen. Mit ihrer Hilfe möchte ich die Lage von Objekten in meiner Umgebung beschreiben. Schließlich möchte ich vorher wissen wie weit ich ´gehen´ muß, um von meinem Standort zu einem bestimmten anderen Ort im Raum zu kommen.“
„Stimmst du mit Poincaire überein, der den Raum als die gedankliche Aneinanderreihung von Körpern bezeichnet?“
Paul wiegt zustimmend den Kopf.
„Maßstäbe, “ murmelt Vasco,„welche Maßstäbe würdest du denn in unserer Situation vorziehen, die Maßstäbe der Heidelberg oder die der Erde??“
„Diejenigen, die ich zur Verfügung habe.“ antwortet Paul prompt.
„Poincaires Definition von Raum,“ fährt Vasco fort, „trifft die geläufige, alltagsnahe Vorstellung. Wir verwenden bewußt oder unbewußt immer einen körperlichen Eichmaßstab für die Bemessung eines Abstandes im Raum. Ein Körper hat die Dimensionen Länge, Breite, Höhe. Wenn wir den Rauminhalt in Vielfachen von Eichkörpergestalten angeben, dann hat Raum zwangsläufig die gleichen Dimensionen wie unsere Eichkörper: Länge-Breite-Höhe.“
„Richtig, Vasco. Wir messen ja den Raum aus, indem wir gedanklich Eichkörper solange aneinander reihen, bis der Raum vollständig ausgefüllt ist.“ Paul nickt zuversichtlich mit dem Kopf.
„Diese Eichkörper, das sind im einfachsten Fall Würfel. Die Kanten wirklicher Körper erkennen wir an der Undurchdringlichkeit des Materials,“ Paul stockt, „aber Körper bestehen aus Elementarteilchen, Vasco!“
Paul hebt freudig den Kopf und fragt mit hintergründigem Lächeln: „Hat zu Zeiten dieses Poincaire jemand daran gedacht, daß Bewegung gegenüber dem Hintergrund die Wechselwirkungsfigur der Elementarteilchen beeinflussen könnte?“
Vasco hüstelt überrascht und zieht die Mundwinkel nach unten. „Mit an Sicherheit grenzender Wahrscheinlichkeit ahnte Poincaire nichts davon.“ entgegnet er vorsichtig.

Sie schienen sozusagen in Bewegungsrichtung länger zu sein, als Ruhende!

Und, da die Eichkörper auch aus Elementarteilchen bestehen, könnte dieser Umstand doch Auswirkungen auf die aus Elementarteilchen zusammengefügten Maßstäbe haben!
Vielleicht sind diese dann auch in Bewegungsrichtung länger ??“

Paul lehnt sich nachdenklich zurück.

„Das ist ja interessant! Die Breite bewegter Elementarteilchen wird wohl nicht verändert - aber die Länge!“ wiederholt er seine Gedanken.

„Was wären die Folgen, wenn die Länge eines bewegten Masstabes in der Bewegungsrichtung größer ist, als die Länge desselben, aber ruhenden Masstabes?“

Paul kritzelt hastig in seiner Skizze herum, legt sie aber schnell wieder beiseite und greift sich ein neues Blatt. Er flüstert: „Der Raum ist die gedankliche Aneinanderreihung von Körpern - also Würfeln, deren Kontur sich aus der Länge der Wechselwirkungsfigur in Bewegunsrichtung ergibt ...“ und zeichnet eifrig.

„Rechts in meiner Skizze mißt ein bewegter Beobachter den Abstand zwischen zwei vor ihm im Raum liegenden Punkten mit sienen Würfeln. Der Linke Beobachter aber ruht. Er hat deswegen kürzere Würfel und er wird deshalb zwischen die Punkte A und B viel mehr seiner Würfel legen können, als der bewegte Beobachter. Das, “ Paul zeigt auf seine Skizze und reibt sich die Hände, „riecht sehr nach Längenkontraktion. Meinst du nicht, Vasco?“

„Hmmm.“ ist alles, was Vasco im Moment dazu äußern möchte.

„Wenn ich Raum als die gedankliche Aneinanderreihung von Körpern auffasse, dann ist der Abstand zwischen zwei Objekten im Raum eine Funktion der Körpergestalt! Das ist ganz klar, Vasco, und es ist sogar eine ganz triviale Sache.
Wenn man zuläßt, daß die Maßstäbe des Beobachters von dessen Bewegung vor dem Hintergrun abhängig sein können, dann wird eine ganz andere Interpretation der Längenkontraktion möglich!
Wenn der zum Hintergrund ruhende Beobachter zum Beispiel 8 Würfel hintereinander legen kann, dann wird der bewegte Beobachter vielleicht nur 4 seiner Würfel dazwischen bringen. Dem Bewegten erscheint der Raum verkürzt!“

„Der Bewegte empfände in diesem Fall eine Längenkontraktion.“ bestätigt Vasco ohne in Pauls Begeisterung einzustimmen.
„Es gibt da natürlich noch ein paar weitere Aspekte, zum Beispiel was dieser bewegte empfindet, wenn er in die entgegengesetzte Richtung schaut, aber ...“

„Ich hätte nie gedacht, daß das so einfach ist!“ unterbricht ihn Paul.
„Immer und immer wieder habe ich gefragt, bin euch ´auf den Nerv´ gegangen, Vasco, woraus die Längenkontraktion ´entsteht´, doch keiner konnte es mir plausibel erklären. Und nun komme ich von selbst darauf!“

„Übertreib doch nicht so!“ dämpft Vasco Pauls Optimismus. „Du hast schließlich schon Jahre lang gewußt, daß es Längenkontraktion gibt.
Neu ist dir doch nur, daß man ihr Zustandekommen mit einem ´Bild´ veranschaulichen kann.
Das Bild erscheint dir zwar einleuchtend, aber das ist es nur, weil du als ´Kompaß´ für eine Bewegung Jonas´ Hintergrundsystem verwendest.
Dieser Kompaß ist aber ein fiktiver! Wenn du die Relativität der Bewegung beider Beobachter deiner Betrachtung voranstellst, dann wird die so einleuchtende Längenkontraktion auf einmal wieder zum Mysterium. Versuche doch einmal,“ Vasco kichert, „einem von beiden Beobachtern zu beweisen, daß er nur zu anderen Werten für die Abstände des ihn umgebenden Raumes kommt, weil er ´falsche´ Maßstäbe benutzt!“

Paul ahnt, daß dies nicht gelingen wird, doch er versucht es natürlich trotzdem.

„Um dies zu beweisen müßte ich die Maßstäbe direkt miteinander vergleichen. Dazu kann ich dem bewegten Beobachter befehlen anzuhalten und seine Würfel neben die Ruhewürfel zu legen. In seinem System ist zwar nach dem Bremsen die Physik genau die Gleiche wie vorher,“ Paul lacht. „aber der ehemals bewegte Beobachter wird feststellen, daß seine Würfel nun exakt genauso lang sind, wie die des Ruhebeobachters. Beide können den Abstand zwischen A und B getrost nochmals messen - sie werden übereinstimmende Ergebnisse bekommen. Der vorher noch registrierte Unterschied ist nicht mehr da!

Du hast recht, Vasco.“ stöhnt Paul. „Der Abgebremste hat keinen physikalischen Anhaltspunkt dafür, daß er sich nun natürlicher bewegt als vorher. Er registriert nur, daß er in seinem neuen Bewegungszustand andere Abstände für an sich bekannte Objekten im Raum findet, als vorher. Da aber die Physik an Bord nach wie vor die gleiche ist, kann er kein ´inneres´ Geschehen für diese Raumdeformation verantwortlich machen. Zumindest kann er nichts dergleichen beweisen.“ Paul schaut Vasco offen an.

„Auch wenn ich dem ruhenden Beobachter sage er soll sich beschleunigen und sich neben dem bewegten Beobachter platzieren, dann wird er dort nur feststellen, daß die beiden Masstäbe gleich groß sind.

Der ehemals Ruhende wird vielleicht stutzig, weil der zuvor gemessene Abstand zwischen den in der Bewegungsrichtung liegenden Objekten A und B nun geringer ausfällt. Es verblüfft ihn bestimmt auch, daß die Abstände in die Gegenrichtung plötzlich größer zu sein scheinen.
Doch auch er findet innerhalb seines Systems nach wie vor die gleiche Physik.
Auch er kann nicht beweisen, daß die alten Werte irgendwie richtiger oder natürlicher sind, als die Neuen.

Ich fürchte, selbst ich würde die Versuche etwas in dieser Richtung zu beweisen, irgendwann entnervt einstellen.“

„Wahrscheinlich.“ kichert Vasco mit Genugtuung. „Du befürchtest also, daß es kein physikalisch verwertbares Kriterium gibt, mit dem wir den einen gleichförmigen Bewegungszustand von dem anderen gleichförmigen Bewegungszustand unterscheiden können.“

„Hmmm!“ knurrt Paul unwillig, denn er hat noch nicht ganz aufgegeben.

„Da die Physik innerhalb der Systeme gleich bleibt, können wir nur die vor einer Beschleunigung gemachten Feststellungen über die Beschaffenheit der Umgebung mit den Feststellungen danach vergleichen. Wenn aus den Datensätzen dann ein Datensatz besonders herausstechen würde, dann wäre das vielleicht ein Hinweis.“ Paul schaut Vasco fragend an.

„Ich weiß zwar noch nicht woran, aber irgendwie müßte man doch ein wirklich ruhendes Elementarteilchen an seiner extremen Oszillationsfigur erkennen können. Vielleicht sind die Maßstäbe für Länge an ihm extrem klein oder , ...“
Paul stockt und betrachtet den Fußboden vor sich. „Extrem, ...“ wiederholt er nachdenklich.

„Nicht nur die Längen wären in diesem System vieleicht extrem, sondern auch die Zeit!“ Paul legt den Kopf in den Nacken und überlegt.
´Zeit ist die Dauer eines Prozesses ´ erinnert er sich an Elis Zeitbegriff. ´Zeit ist eine Dimension´ - das sagte Einstein.

Was wäre nun bei Jonas der Maßstab der Zeit?

Der Maßstab für Länge, Breite Höhe erwächst bei Jonas aus der Wechselwirkungsfigur der Elementarteilchen.
Die Längenmaßstäbe waren in den verschiedenen Richtungen nicht gleich - sie hingen davon ab, ob man sich in oder gegen die Bewegungsrichtung orientierte. Aber sie waren immer eine Funktion der Geschwindigkeit des Teilchens vor dem Hintergrund.

In Anlehnung an Elis Definition sollte Paul nun nach dem Prozess suchen, den er zum Maßstab der Zeit erheben könnte.
Halt! Paul korrigiert sich: Er sollte nach dem Prozess suchen, dessen Dauer er zum Maßstab der Zeit machen könnte.

„Wir brauchen einen elementaren Standardprozeß für die Zeit.“ verkündet er leise seine Erkenntnis.

„In unseren Quarzuhren ist zum Beispiel dann eine Sekunde abgelaufen, wenn eine ganz bestimmte Anzahl von Schwingungen im Quarzkristall der Uhr erfolgt sind. Der Standardprozeß dabei ist ein Schwingungszyklus der im Quarzkristall schwingenden Elektronen.
Die Dauer eines solchen Schwingungszyklus bildet den elementaren Zeitmaßstab der Quarzuhr.“

Vasco nickt schweigend und wartet - er ließ Paul ZEIT.

„Die räumlichen Maßstäbe - ich meine jetzt die drei Längendimensionen der Elementarteilchenoszillation -sind ja etwas sehr elementares.
Da wir die Eigenschaft der Jonas-Elementarteilchen dreidimensionalen Raum ´in Anspruch zu nehmen´ zum Maßstab des umgebenden Raumes gemacht haben, liegt es auf der Hand nach einer weiteren Eigenschaft dieser Teilchenoszillationen Aussschau zu halten, deren Dauer uns den Maßstab der Zeit liefert.

Ich denke dabei an die Zyklusdauer einer Elementarteilchenwolke, Vasco.
Ich meine damit nicht die einzelnen internen Zick-Zack-Bewegungen des Inneren Urobjektes. Dessen Bahnen sind zwar auch in gewissem Maße regelmäßig - zumindest, wenn man lange genug hinschaut -aber als charakteristischer Prozeß im Elementarteilchen, schwebt mir ein kompletter Wechselwirkungszyklus des Inneren Urobjektes vor.
Im Verlauf dieses Prozeses soll sich das gesamte Spektrum der teilchenspezifischen Wechselwirkungen mit der Umgebung widerspiegeln. Der Zyklus steht damit für die Gesamtheit der Teilcheneigenschaften - all der Eigenschaften, die für uns das Teilchen ´erlebbar´ machen ...“

„ Hmmm!“ mehr war von Vasco nicht zu hören.

„Ich möchte die Dauer all der Einzeloszillationen zum Maßstab der Teilchenzeit machen,“ wiederholt Paul, „die nötig sind um alle teilchenspezifischen Wechselwirkungen mit der Umwelt herauszubilden.“
Paul glaubt es endlich auf den Punkt gebracht zu haben. Er lehnt sich erwartungsvoll zurück.

Dafür reibt sich Vasco heftig das Kinn.

„Die Dauer all der Oszillationen, die die Teilcheneigenschaften ....“ wiederholt er und kratzt sich verzweifelt am Scheitel.
„Die Frage, wann diese Eigenschaften vollständig abgebildet sind, die kann ich mir bestimmt sparen. Das ist der gleichen Zirkel wie die Frage nach dem Vorfahren der Henne und dem Ei,“ er kichert leise.
„Möglicherweise ist das mit den Teilcheneigenschaften aber gar keine schlechte Zeit-Definition. Was hätte denn solch ein ZEIT-Maßstab für Konsequenzen, Paul. Passen sie zur Wirklichkeit?“

„Ich hoffe doch.“ antwortet Paul optimistisch. „Da sich die Längenmaßstäbe entsprechend der Bewegung des Teilchens zum Hintergrund verändern, müßten sich auch die Zeitmaßstäbe verändern. Bei Jonas sind bewegte Elementarteilchenoszillationen pauschal gesagt länger als ruhende. Sie brauchen deshalb auch länger für einen Zyklus.“

„Die Frage ist nur, warum ??“ wirft Vasco dazwischen.

Paul dreht sich langsam um und schaut ihn nachdenklich an.
„Vielleicht kann ich das an einem kosmischen Beispiel veranschaulichen.“ entgegnet er nach einer Weile.
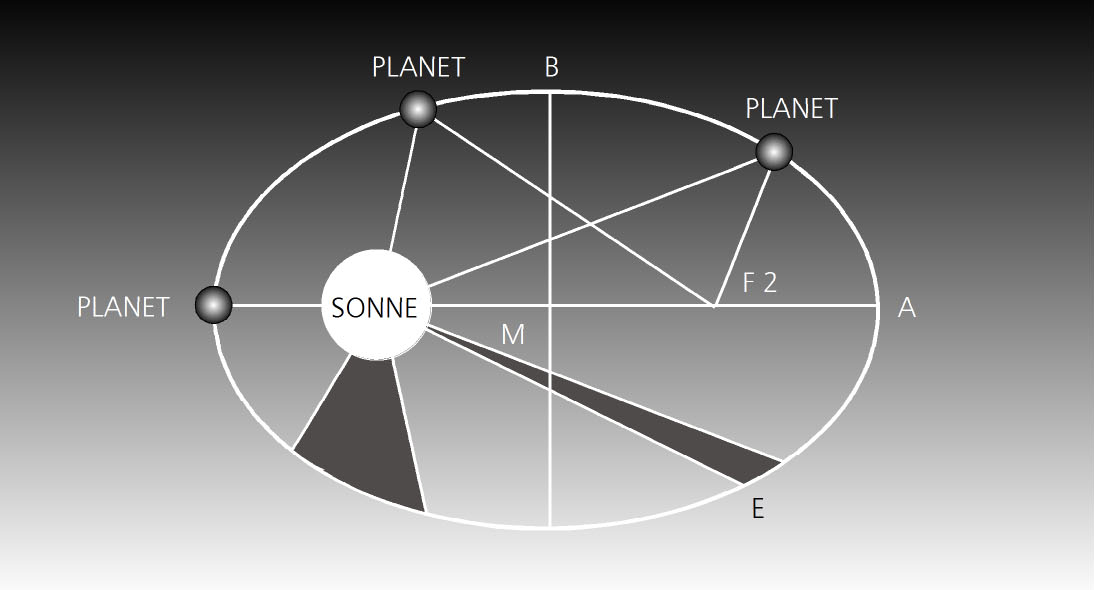
„Meinem Zeitmaßstab - der Zyklusdauer einer Teilchenoszillation - möchte ich die Umlaufdauer eines Planete, der um seinen Zentralstern, seinen Attraktor umläuft, gegenüberstellen.
Ein solcher kompletter Umlauf ist ebenfalls ein Zyklus - die dafür benötigte Zeit, ist eine Zyklusdauer.

Johann Kepler hat entdeckt, daß die Umlaufzeit von Planeten um so größer ist, je länger die großen Halbachsen seiner Bahn sind.
Andererseits ist die Länge der Halbachsen auch ein Ausdruck der im Planeten enthaltenen Bewegungsenergie - bezogen auf Newtons Raum.

Sylvia sagte mir, daß wir bei der Berechnung von Satellitenpositionen davon ausgehen, daß die Summe der potentiellen und kinetischen Energie an allen Punkten der Satellitenbahn gleich groß ist.

Je größer diese Summe ist, desto räumlich länger ist die Ellipsenbahn und desto länger wird ein Umlauf um den Attraktor des Planeten, das Zentralgestirn, dauern.“ Paul blinzelt Vasco zuversichtlich an.

„Diese Umlaufdauer ist auch keine Frage der Masse des Satelliten, sondern sie ist lediglich eine Funktion der in ihm enthaltenen Energie. Verändert man diese, dann wird sich das unweigerlich in einer veränderten Umlaufdauer niederschlagen.

Übertrage ich diesen Zusammenhang auf meine Elementarteilchenschwingung, dann sollte ich ebenfalls mit einer Veränderung der Zyklusdauer rechnen, wenn ich die Innere Energie des Urobjektes verändere.
Das Urobjekt eines vor dem Hintergrund sehr schnell bewegten Elementarteilchens enthält mehr Energie als das von Ruhenden - demnach müßte der Zeittakt in ihm langsamer ablaufen als beimRuhenden.
Auch in den Elementarteilchen der schnellen Heidelberg ist viel Energie enthalten, da sie von den Raumschiffantrieben kräftig beschleunigt wurden.
Wenn die Heidelberg schnell unterwegs ist, müssten die Oszillationsfiguren länger sein und - in Analogie zu Kepplers Gesetzen - deshalb sollte auch ihr Zyklus länger dauern, ihr Zeittakt wäre also ebenfalls gedehnt.

Und, wenn ich mich recht erinnere,“ Paul lächelt siegessicher, „ticken die Uhren auf der schnellen Heidelberg tatsächlich langsamer als die auf der langsamen Erde. Hier brauchen sie offenbar für einen TICK länger - wegen der Zeitdilatation. “

Kepplersche Gesetze

1. Die Bahnen der Planeten sind Ellipsen, in deren einem Brenn-punkt die Sonne steht.

2. Der Fahrstrahl von der Sonne zum Plane-ten überstreicht in gleichen Zeiten gleiche Flächen.

3. Die dritten Potenzen (Kuben) der großen Halbachsen der Planetenbahnen verhalten sich wie die Quadrate der Umlaufzeiten.

aus: Bertelsmann Universallexikon 1995

Paul hat die Augen geschlossen „Langsam glaube ich zu verstehen, was Jonas damit meinte,“ murmelt er und wiederholt dann ein paar Zeilen aus dem Artikel: „...erst die aus ihrer Gestalt und ihrer zeitlichen Existenz ableitbaren Relationen zu anderen Elementarteilchen führen zu dem, was wir als Dimensionen bezeichnen - Zeit und der Ausdehnung.“ Paul atmet tief durch.

„Natürlich. Je schneller sich ein Elementarteilchen gegenüber dem Hintergrund bewegt, desto länger werden die in die Bewegungsrichtung zeigenden Maßstäbe sein - und desto langsamer werden seine Uhren ticken.

Der Energiegehalt eines jeden Teilchens spiegelte sich in dessen Wechselwirkungsfigur wider. Diese Gestalt ist aber nicht rein ´räumlich´, sondern sie ist auch in gleichem Maße ´zeitlich´, denn sie ist nicht ohne Zyklus denkbar.

Sowohl der Längenmaßstab als auch der Zeitmaßstab wären dann aber nur verschiedene Abstraktionen aus ein- und derselben Wechselwirkungsfigur. Die so häufig zitierte Einheit der vier Dimensionen wird damit zu einer Selbstverständlichkeit. Und ...“
Paul springt plötzlich auf, „wenn ich diesen Raum-Zeitlichen Zusammenhang in die Poincaire´sche Raumdefinition übertrage, dann entpuppt sich dessen dreidimensional gedachter Raum als unvollständig! Als kastriertes Etwas!“

Paul überlegt kurz, doch dann bekräftigt er seine These. „Es ist so, Vasco! Drei Dimensionen sind einfach zu wenig um die Lage von Körpern ´im Raum´ zu beschreiben. Wenn ein Körper aus Oszillationsfiguren, den Sinnbildern der Einheit von räumlichem und zeitlichem besteht, dann muß Poincaires Raum -die gedankliche Aneinanderreihung von Körpern- auch vierdimensional sein!

Man kann die Zeit nicht isoliert von Länge, Breite Höhe betrachten. Räumliches und zeitliches gehören einfach untrennbar zusammen !“

Ohne eine Miene zu verziehen hat Vasco bisher zugehört. „Vierdimensional!“ wiederholt er nun und hebt den Kopf. „Jonas´ Welt ist also vierdimensional.
Sie sieht damit genauso aus wie die Welt Einsteins : Vierdimensional!
Wahrscheinlich ´siehst´ du sogar einen Unterschied zwischen beiden Welten, Paul.
Die Einheit von Räumlichem und Zeitlichem bei Jonas erscheint dir plausibler, während du sie bei Einstein als eine eher mathematische Schlußfogerung siehst.“
Vasco kichert. „Trotzdem ist Einstein ein paar Jahre früher zu dieser Erkenntnis gekommen und ich glaube, daß er den Jonas´schen Ideen nicht einmal Eingang in seinen Theorien gestattet hätte.

Wozu auch ? Einstein hat schließlich bewiesen, daß er die Zusammenhänge der Relativitätstheorien auch ohne ´gefüllten´ Raum denken konnte... Doch das ist ein Thema für sich.“ schließt er abrupt.

„Die Dimensionen hast du nun, Paul. Die Längenkontraktion und Zeitdilatation auch.
Bis zur Lichtgeschwindigkeit und damit dem Speziellen Relativitätsprinzip scheint es nur ein kleines Stück zu sein aber, so fürchte ich, dieses kleine Stück hat es in sich.