Der Harmonischer Oszillator der QM und der Begriff der Resonanzfigur

Die Beschreibung von Materie als Resonanzfigur ist beabsichtigt anders als der Begriff des Harmonischen Oszillators, der in der QM zur Modellierung schwerer Materie dient. Der Grund dafür liegt darin, dass die QM  Objekte (Materie) als quantenharmonischen Oszillatoren beschreibt, wobei das Oszillieren auf einer angenommenen ´Inneren´ Bindung der am Schwingungssystem beteiligten Objekte beruht. → Federbeispiel von Prof. Harald Lesch hier.  Der harmonische Oszillator der QM oszilliert also sozusagen ´in sich´.

Eine Materiewelle im Sinne dieses Modells ist aber ein Resonanzfigur,  als Ausdruck einer ständigen (und damit das zeitliche Darstellende) Wechselwirkung der Inneren Energie der Materiewelle mit seiner ´Umwelt´.  Beide, Umwelt und innere Energie befinden sich in einem Impulsgleichgewicht und damit in Resonanz zueinander. Dieser Zustand ist Voraussetzung für ihre zeitliche Existenz und damit der Möglichkeit mit ihnen Chemie zu ´machen´.

Für Interessierte hier einige Grundlagen zum harmonischen Oszillator der QM aus dem Netz:

Die Chemiker sehen es z.B. so:

In der Molekülphysik erlaubt er (der harmonische Oszillator – Anm. des Verf.) eine Näherung der Bindungsverhältnisse zwischen Atomen und ermöglicht so z. B. eine Vorhersage über Schwingungsspektren. Dies lässt sich verdeutlichen, indem eine Bindung durch zwei über eine Feder (harmonisches Potential) miteinander verbundene Massepunkte (die Atome), die gegeneinander schwingen, dargestellt wird:

Die lineare Rückstellkraft F(x) einer solchen Feder führt auf ein harmonisches Potential V(x) (proportional x²) und somit auf den harmonischen Oszillator. In realen Molekülen sieht das Potential etwas anders aus, aber der harmonische Oszillator ist, zumindest für niedrige Schwingungsenergien, eine gute Näherung.

• Ein weiteres Beispiel ist die Torsionsschwingung des Ethylenmoleküls, die in der folgenden Zeichnung dargestellt ist: Dabei verdrillt sich sozusagen die Doppelbindung und jeweils zwei Wasserstoff-Atome schwingen drehend gegeneinander.

• In der modernen Atomphysik werden zu untersuchende Atome und Ionen in optischen Fallen bzw. Ionenfallen gefangen und gekühlt, um z. B. bei Messungen eine höhere Auflösung zu erhalten. Außerdem kann man in solchen Fallen neue Zustände der Materie untersuchen (z. B. Bose-Einstein-Kondensate, Fermi-Kondensate). Solche Fallen weisen ein, in erster Näherung, parabolisches Potential auf. Somit können Teilchen in diesen Fallen ebenfalls mit dem Modell des quantenmechanischen harmonischen Oszillators beschrieben werden.
  
  

• In der Festkörperphysik beschreibt das Einstein-Modell (nach Albert Einstein) eine Methode, um den Beitrag der Gitterschwingungen (Phononen) zur Wärmekapazität eines kristallinen Festkörpers zu berechnen. Grundlage ist die Beschreibung des Festkörpers als aus N quantenharmonische Oszillatoren bestehend, die jeweils in drei Richtungen unabhängig schwingen können.

Nullpunktsenergie

    Das obige Ergebnis hat fundamentale Folgen: Der harmonische Oszillator kann nicht mehr beliebige                     Energiemengen aufnehmen, sondern nur ganzzahlige Vielfache von .

 Der Zustand mit der niedrigsten Energie ist . Daraus folgt, dass ein quantenmechanischer harmonischer Oszillator selbst am absoluten Temperaturnullpunkt noch die Energie E₀ besitzt.

Im klassischen Fall dagegen ist die Temperatur ein Maß für die Energie pro Freiheitsgrad des Systems. Am absoluten Nullpunkt sollte dementsprechend die Energie gleich null sein.Hier liefert die Quantenmechanik ein offensichtlich im Widerspruch zur klassischen Vorstellung  stehendes Ergebnis, welches aber tatsächlich eine korrektere Beschreibung der Natur darstellt.

Dies äußert sich auch darin, dass die  Aufenthaltswahrscheinlichkeit für n = 0 eine nicht- verschwindende Breite hat. Das Teilchen ist also nicht exakt bei x = 0 lokalisiert, wie man es von einem klassischen Oszillator erwarten würde. Diesen Sachverhalt nennt man auch Nullpunktschwingung, bzw. Nullpunktsenergie.

Man kann diesen Sachverhalt auch mit der Heisenbergsche Unschärferelation beschreiben. Im klassischen Fall hat das oszillierende Teilchen     die exakte Position x = 0 und den exakten Impuls p = 0. In der Quantenmechanik besitzt ein Teilchen keinen exakten Ort und keinen exakten Impuls.

Die Standardabweichung beider Observablen ist über die Unschärferelation verknüpft. Daher kann der Ort und der Impuls des Teilchens nur bis zu einer gewissen Grenze gleichzeitig angegeben werden. Dies lässt sich als Art räumliche „Verschmierung“ beschreiben, welche eine kinetische Mindestenergie des Teilchens zur Folge hat.

 Dass in der quantenmechanischen Beschreibung auch außerhalb des harmonischen Potentials eine Aufenthaltswahrscheinlichkeit für das Teilchen existiert, liegt daran, dass das Teilchen durch die endlich hohe Potentialwand getunnelt werden kann (siehe Tunneleffekt).

  Gegenüberstellung Resonanzfigur <->Oszillator

Der inhaltliche Unterschied zwischen den mit den beiden Begriffen dargestellten Objekten besteht m.E. in dem Umstand, dass beim Oszillator der QM (aus bestimmten Gründen) eine Wechselwirkung mit der Außenwelt ausgeschlossen wurde. Es wird her eine ´innere´ Bindung angenommen. Die Kerne werden von Gluonen zusammengehalten, die zwischen den Kernbausteinen (den Quarks) hin- und herflitzen und sie schier untrennbar aneinander ketten. Das Bild unten zeigt das Prinzip der Gluonenbindung:

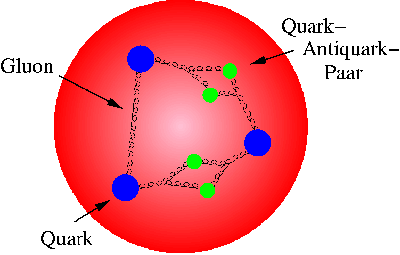
In der Darstellung der Materie als Resonanzfigur (= Materiewelle) gibt es aber keine separat denkbaren Objekte wie Gluonen.  Es gibt hier nur die, auf dem Prinzip des Impulsgleichgewichtes zwischen inneren und äußeren Impulsen beruhende Wechselwirkung zwischen dem Impuls tragenden Objekt der geschlossen schwingenden Materiewelle und denen des Hintergrundes.

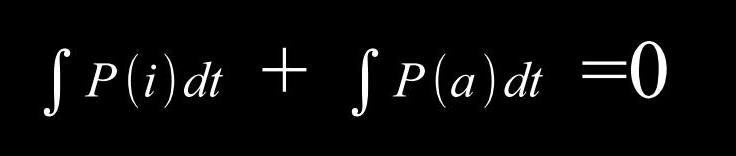
Nach dieser Sinne sind Gluonen also verwaschene Raumbereiche (wie Strudel) anzusehen, die sich als stehende Wellen zwischen den noch dichteren Quarks infolge der wechselseitigen Abschirmung der Quarks vor dem Impulsen des Hintergrundes immer neu herausbilden. Es sind also Bereiche, in denen der Impulsdruck sehr viel geringer ist als in der Umgebung. Diese Differenz begründet den Zusammenhalt der Schwingungsfigur. Diese ist nur als Gesamtheit denkbar. Man kann keines ihre Elemente abrennen ohne damit die Gesamtheit zu zerstören.  -> Bild unten aus der Mitte, in dem Gluonen nicht mehr dargestell sind.

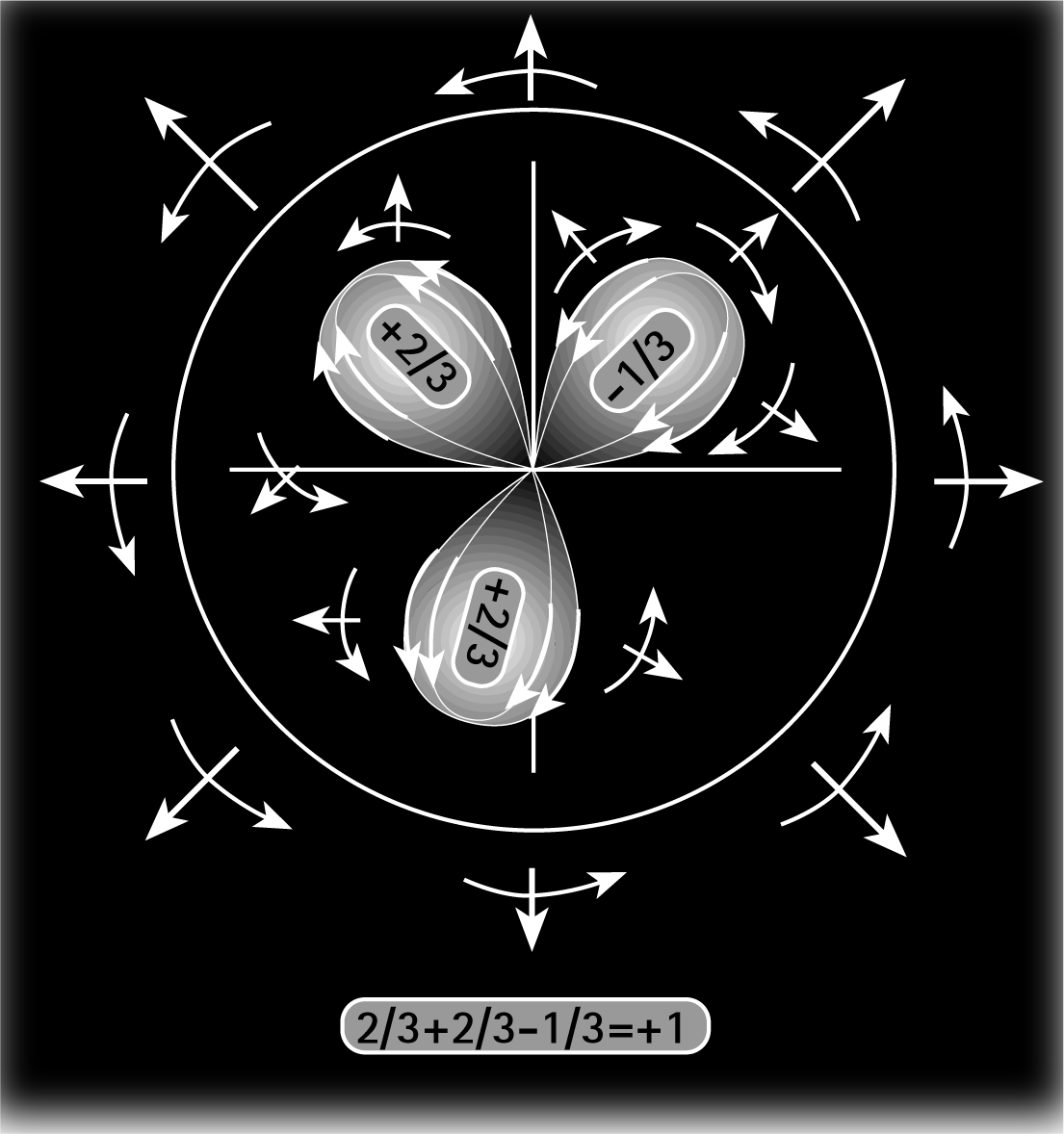
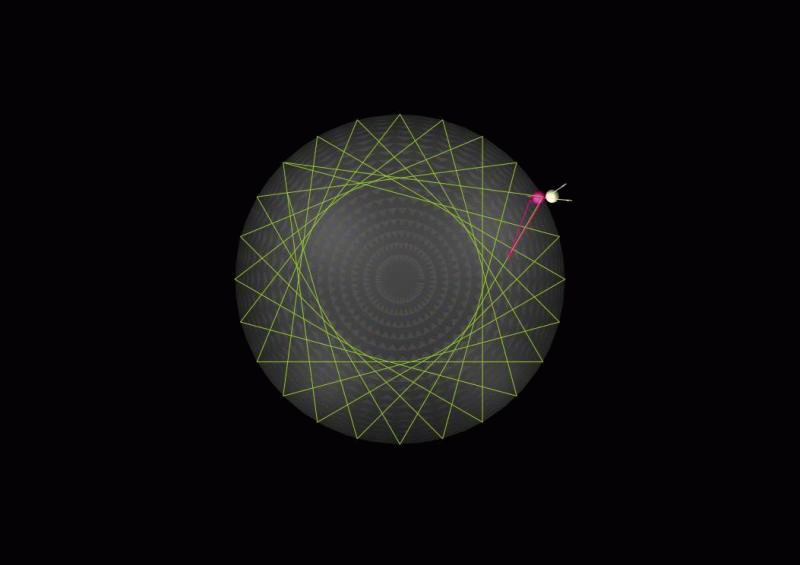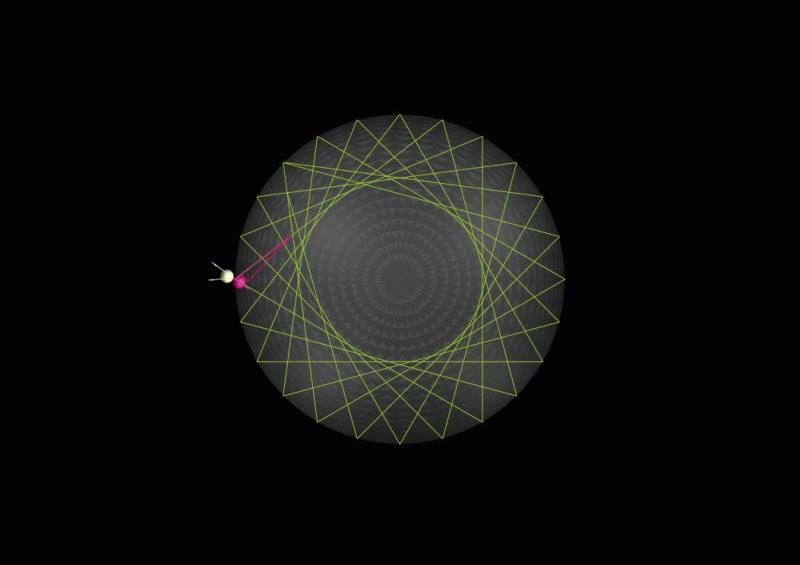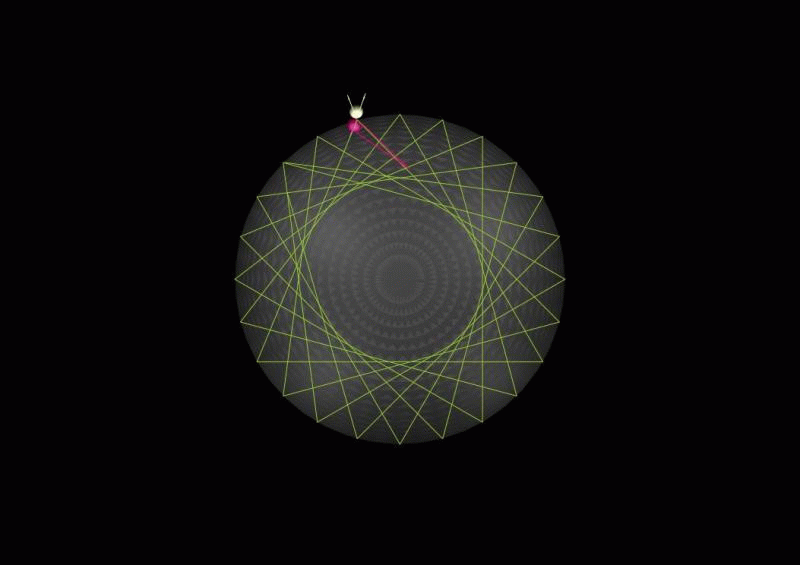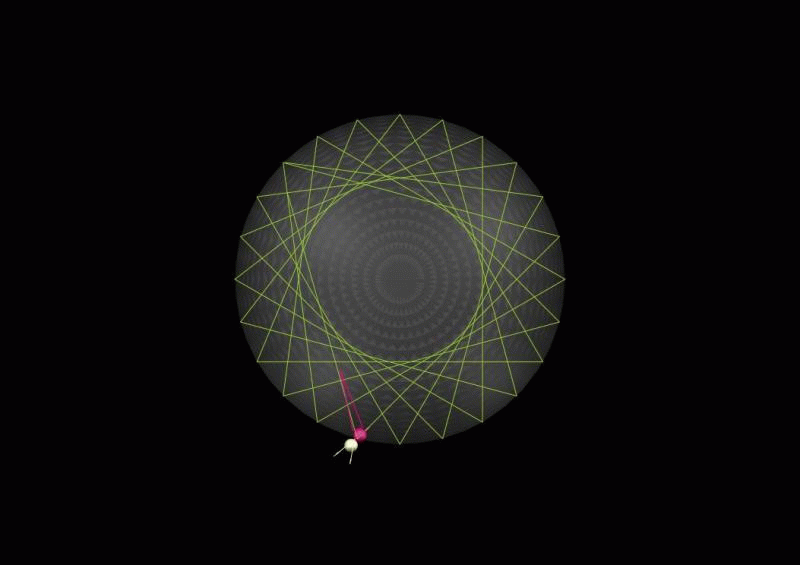
das Bild veranschaulicht das Prinzip der WW der Figur mit der lokalen Umwelt. Wobei die Quarks selbst auch nur als Resonanzfiguren wie im Bild unten aufzufassen sind,  die nur markanter erscheinen als die sie verbindenden weniger dichten Gluonenwirbel.

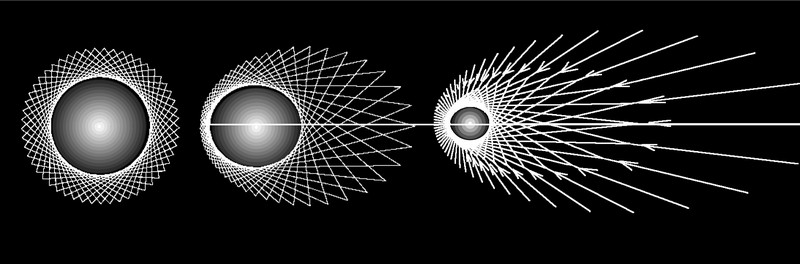
Ein Blick auf die einfache Darstellung einer Resonanzfigur in Ruhe zum lokalen Hintergrund (links)  und gegenüber dem lokalen Hintergrund in Bewegung (rechts),

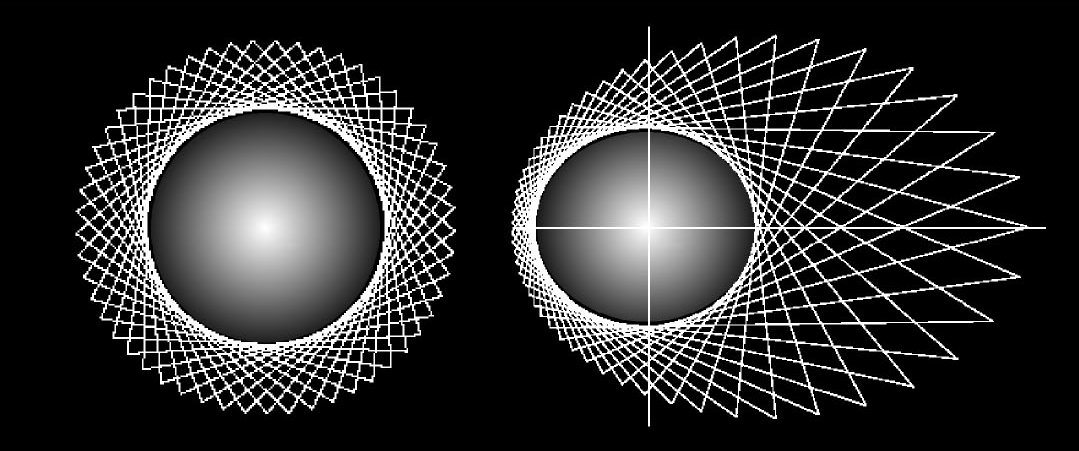
lässt eine plausible Folge der Schwingungsdynamik zwischen Innen und Außen erkennen, die als Heisenbergsche Unschärfe bekannt ist, wobei beide Zustände sich zu diesem Hintergrund im Gleichgewicht befinden.

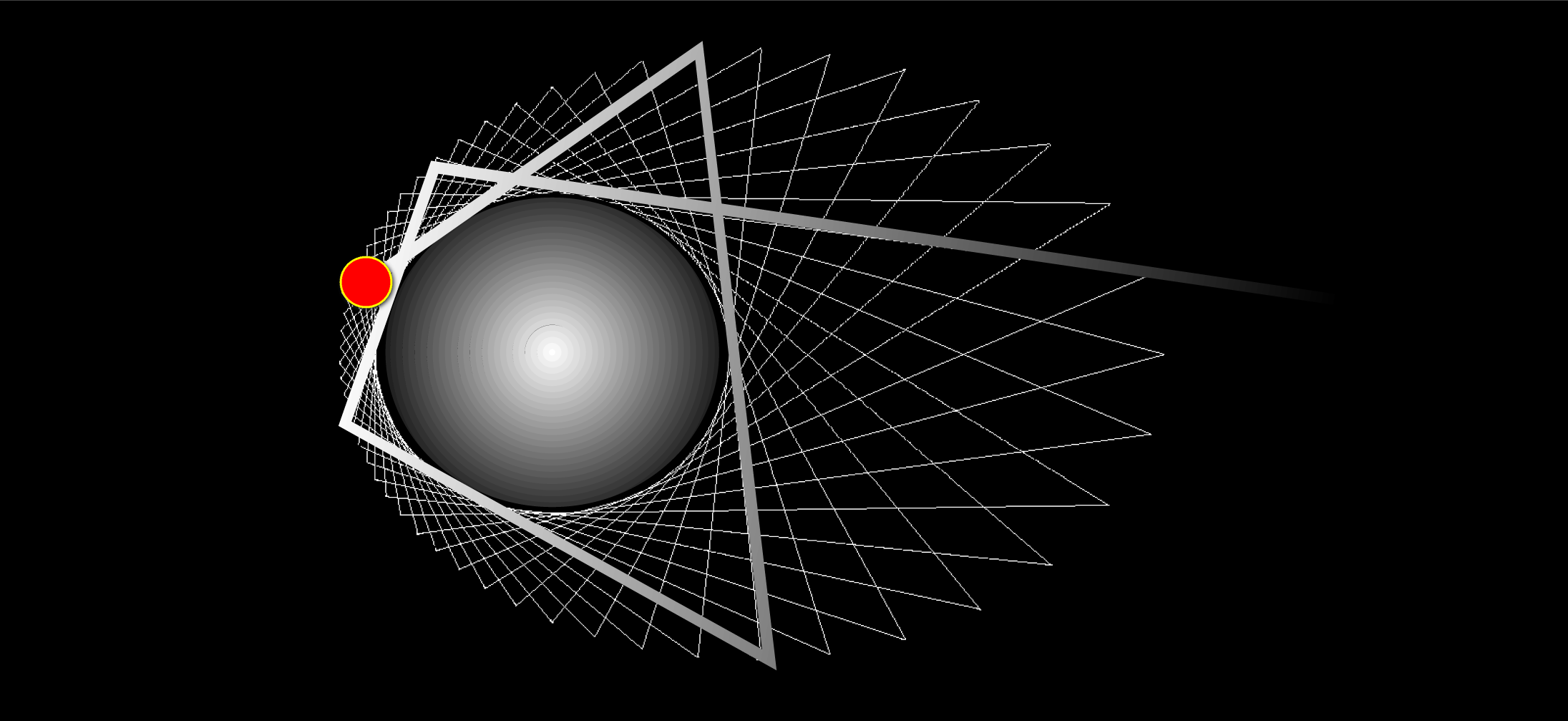
Erst eine Vielzahl der Bahnen der oszillierenden / resonanten Objekte bilden ein ´Teilchen´, eine Resonanzfigur, mit der ´Chemie gemacht´ werden kann. Im Falle des Elektrons im Doppelspaltversuch ist dieses zunächst als Wellenpaket unterwegs und geht (wenn nicht gestört ->beobachtet) durch beide Spalte. Die Materialisierung des bis dahin ausgedehnten Wellenpaketes am Schirm erfolgt dann aber in ein vergleichsweise winziges Atom hinein.
Wir können die einzelnen Schwingungen des Elektrons auf seinem Weg durch das Vakuum nicht sehen und deshalb auch nicht vohersagen, an welcher Stelle des Schirmes das im ausgedehnten Wellenpaket oszillierende Objekt auftreffen wird. Es kann zwar eine Region vorhergesagt werden, aber der konkrete Ort, an dem die ´Wellenfunktion zusammenbricht´ kann nur statistisch für eine bestimmte Zielregion angegeben werden.

Aber es gibt noch viel mehr Fragen...