Dies ist die Physikseite
Auszug 3 aus Überall ist die Mitte (2003)
Die Lichtgeschwindigkeit
Maxwell fand bereits im 19. Jahrhundert, dass die Konstanz der Lichtgeschwindigkeit ein fundamentales Element seiner Gleichungen ist. Für ihn war dieses Ergebnis plausibel, denn er glaubte damals noch an den Lichtäther, in dem sich diese Wellen ausbreiten sollten.
Der Spezielle Relativitätstheorie 1904 (SRT) betrachtet auch die schwere Materie und sie hat die Konstanz der C ebenso zur Grundlage - aber diesmal ohne Äther. So paradox uns diese Konstanz zunächst erscheint, so ergibt sie sich am Ende als logische Konsequenz der Beziehung zwischen Materie und Raum. Sie werden sehen:
Kapitel: Die Lichtgeschwindigkeit S.148ff
Die Lichtgeschwindigkeit
Du kennst zwar den Michelsonversuch, Paul, aber die geometrische Darstellung des Zustandekommens der Urgleichung der Lorentztransformation ist dir bestimmt nicht bekannt.“
Nach einer Sekunde ist sie 300 000 km davon geeilt.
Die Kugelgestalt dieser Lichtwelle kann jeder Oberschüler mathematisch beschreiben: x² +y² + z²- T² = 0 - lautet die Gleichung, wobei T der momentane Abstand zwischen der Wellenfront und ihrem Ursprung ist - der Blitzlampe.
Dieser Abstand wächst mit der Zeit t, da sich Licht schließlich mit c bewegt. Wir können also für T genauer schreiben: T = c* t, wenn wir die Zeit t, die seit dem Aussenden des Lichtblitzes vergangen ist, verwenden.“

Vasco schaut Paul prüfend an und fährt dann mit zuversichtlicher Mine fort.
„Nun betrachten wir diese Lichtwellenfront von einem anderen Bezugssystem aus, nämlich einem, daß sich gegenüber der Blitzlampe bewegt.
Da in beiden Gleichungen auf jeweils einer Seite die „0“ steht, kann ich sie gleich nebeneinander schreiben:
X(1)²+Y(1)²+Z(1)+c²*t²= X(2)²+Y(2)²+Z(2)²+c²*t²
Dies ist die Gleichung, in der man das Ergebnis des Michelsonversuches formuliert. Diese Gleichung verbunden mit einem Erhaltungssatz gestattet einem Physiker die Spezielle Relativitätstheorie abzuleiten. Zumindest sollte er das können.
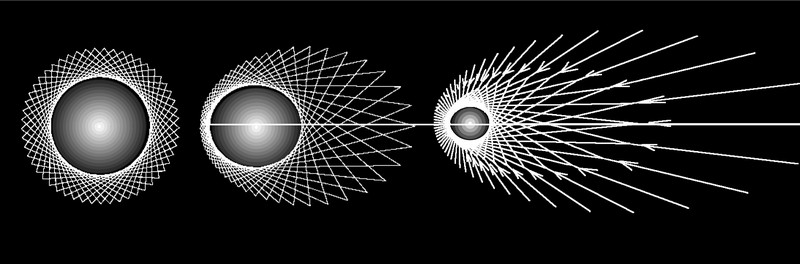
In meiner Skizze habe ich die davon eilende Lichtwellenfront zu drei Zeitpunkten dargestellt. Die mit BS bezeichneten Orte neben dem Zentrum verkörpern die jeweilige Position des bewegten Bezugssystems.”
Paul beugt sich über Vascos Zeichnung und fragt: “Und von jedem der beiden Bezugssysteme sieht der Beobachter diese Lichtwellenfront mit C davoneilen?”
Vasco nickt. Doch Paul schüttelt schließlich ablehnend den Kopf.
“Möglich, daß diese Gleichung die Konstanz der Lichtgeschwindigkeit beschreibt. Sicherlich. Doch ich kann aus dieser Gleichung, und auch aus dieser Darstellung nicht entnehmen, weshalb die Lichtgeschwindigkeit von beiden Beobachtern als gleich gesehen wird. Doch vielleicht geht es besser, Vasco, wenn wir die unterschiedlichen Maßstäbe berücksichtigen! Bei Jonas hat ja der bewegten Beobachter andere Maßstäbe, als der Ruhende ,... ”
Paul greift rasch nach Vascos Block, reißt die Skizze ab und wendet das Blatt und erklärt: “Das Blatt Papier, Vasco, das verkörpert das ruhende System. Vom Bildrand rechts und links dringen zwei Lichtwellenfronten ein. ..

Sie bewegen sich auf das in der Mitte ruhende Teilchen zu. Das Teilchen wird beide Lichtwellenfronten gleich schnell näher kommen ´sehen´, denn da es ruht, ist es ´rund´. Es verwendet deshalb sowohl nach links als auch nach rechts gleich große Maßstäbe.”
Paul schaut Vasco prüfend an. Vasco nickt - wortlos.
“Die Wechselwirkungsfigur eines bewegten Teilchens, die sieht aber anders aus.” Eifrig zeichnet Paul eine weitere Skizze neben die erste.

“Im ersten Moment glaubt man , daß auch hier das bewegte Teilchen die nacheilende Lichtwelle als langsam, und die von vorn kommende Lichtwelle als schnell empfindet. Doch das ist ein Trugschluß!
Man muß nämlich die vom Teilchen erlebte Annäherungsgeschwindigkeit der Lichtfronten auf die dem Teilchen eigenen Längen- und Zeitmaßstäbe beziehen! Und die sind bei Jonas abhängig von der Geschwindigkeit gegenüber dem Hintergrund!
Wenn die Teilchenmaßstäbe in der ganzen Welt und bei allen Bewegungszuständen unveränderlich wären, dann wäre die klassischen Addition der Geschwindigkeiten nach Galileo immer richtig. Doch dann hätte Michelson falsch gemessen ...”“
Es sei denn,” wirft Vasco dazwischen, “der ´Raum´ würde sich verändern.”
“Michelson hat aber richtig gemessen!” konzentriert sich Paul und wischt Vascos Einwand mit einer abwehrenden Geste beiseite.
“Und weil Michelson richtig gemessen hat, sind entweder die Maßstäbe nicht überall und bei allen Bewegungszuständen gleich, oder der Raum verändert sich immer dann, wenn sich der Bewegungszustand eines Teilchens gegenüber der Welt verändert!”
Paul schaut Vasco lange fragend an. Schließlich schüttelt er nachdrücklich den Kopf.
“Ganz ehrlich, Vasco, ich halte die Variante mit Jonas molluskenhaften Maßstäben für einleuchtender. Es fällt mir einfach schwer zu glauben, daß sich die ganze Welt verändert, nur weil ein Elektron in einem Feld beschleunigt wurde.” Paul schüttelt erneut, und diesmal sehr nachdrücklich, seinen Kopf.
“Doch möglicherweise spielt die Interpretation keine wesentliche Rolle. Ob sich nun der ´Raum´ oder die ´Maßstäbe´ verändern: die mathematische Formel für eine Prognose sieht in beiden Fällen wohl gleich aus.
Wirklich nachvollziehbar wird Michelsons Ergebnis für mich aber, wenn ich die Annäherungsgeschwindigkeit der Lichtwelle auf die subjektiven Längenmaßstäbe der Teilchenwolken nach vorn und nach hinten beziehe. Dann verstehe ich, weshalb einem Teilchen die sich von vorn und von hinten annähernden Lichtwellenfronten als gleich schnell vorkommen.
Für die Geschwindigkeit der von vorn kommenden Lichtwellenfront wird das Teilchen den in dieser Richtung weisenden, vergleichsweise langen Maßstab X(v) verwenden. Und für die Geschwindigkeit der von hinten heraneilenden Lichtwelle wird es den nach Hinten weisenden, vergleichsweise kurzem Maßstab X (R) verwenden.
Die Unterschiede im Maßstab nach ´vorn´ und nach ´hinten´ führen dann dazu, daß die von vorn kommende Lichtwellenfront in einer Zeiteinheit mit X (v) eine scheinbar ´längere´ Längeneinheit zurücklegen muß, als die von hinten nachkommende. Die von hinten nachkommende Front wird deswegen als ´gleich schnell´ empfunden, weil sie in derselben Zeiteinheit mit X(r) ebenfalls eine ganze Längeneinheit zurücklegt.
Wenn nun diese Raum-Zeitlichen Verzerrungen der Teilchengestalt so ausfallen wie es deine Lorentztransformation fordert,” triumphierend weist Paul auf Vascos Zeichnung und die lange Formel. “dann ergibt sich die Konstanz der C in jedem Bezugssystem! Michelson, Lorentz und Fiz Gerald wäre damit doch zufrieden. Oder, Vasco?”
“ Hmmm!” Vasco kratzt sich unsicher am Ohr. Eine derartige Herleitung der Konstanz der Lichtgeschwindigkeit hatte er nicht erwartet.
“Das muß ich mir erst noch einmal durch den Kopf...” gesteht er und lehnt sich zurück. Demonstrativ schließt er die Augen.
Paul geht nervös im Zimmer auf und ab. Er ist schon einer anderen Interpretation für die Konstanz der C auf der Spur.
“Vielleicht kann ich die Sache auch von einem ganz allgemeinen Standpunkt aus betrachten...” murmelt er.
“Bei Jonas empfindet ein im Hintergrund ruhendes Teilchen die Lichtgeschwindigkeit konstant aus allen Richtungen - das ist klar.
Ein dazu gleichförmig bewegtes Teilchen unterscheidet sich vom Ruhenden in seiner Oszillationsfigur.
Die Veränderung der Oszillationsgestalt kompensiert sozusagen exakt die klassisch zu erwartenden Bremseffekte der Bewegung des Teilchens in einem Medium. Die Gestaltänderung ist deswegen ganz klar bestimmt. Jedes Teilchen muß schließlich genau die Oszillationsgestalt annehmen, die seinen Umgebungsbedingungen exakt entspricht. Nur eine absolut hundertprozentige, eine vollständige Anpassung suggeriert dem Teilchen, daß es ´in Ruhe´ wäre.
Und genau deshalb wird jedem gleichförmig bewegten - und damit ja auf ´Ruhe´ getrimmten Teilchen - die Lichtgeschwindigkeit als konstant aus allen Richtungen erscheinen müssen !
So, wie die C einem wirklich ruhenden Teilchen als konstant aus allen Richtungen erscheint, wird sie auch einem bewegten, aber aus ´existenziellen Gründen´ perfekt auf Ruhe getrimmten Teilchen, als konstant aus allen Richtungen erscheinen. Vasco: Licht pflanzt sich schließlich in dem gleichen Strahlungsstrom von Urobjekten fort, in dem auch das unablässig auf ausgeglichenen Impulshaushalt getrimmte Teilchen schwimmt.”
Seine Nase reibend wiederholt Vasco. „Die Oszillationsfigur eines gleichförmig bewegten Teilchens gaukelt diesem also immer vor, daß es in einer isotropen Hintergrundstrahlung ruht ...“ Kopfkratzen.
Dimensionen unter Druck
„Na endlich, “ Paul reibt sich die Hände. „Mir ist eben noch etwas anderes aufgefallen, Vasco. Die Hintergrundstrahlung wirkt auf die in ihr eingebetteten Teilchenwolken so ähnlich wie der Luftdruck auf einen Luftballon.Wenn nun ein durch das All fliegendes Teilchen in einen Raumbereich eindringt, in dem die allseitige Urobjekteströmung aus irgendeinem Grund schwächer ist als in der Gegend, aus der das Teilchen kommt, dann müßte dies an der Teilchenenklave eine erkennbare Wirkung hinterlassen ...“
„Hmm?“
„ ... wenn wir die innere Energie des Elementarteilchenobjektes als gleichbleibend betrachten, dann müßte zum Beispiel eine Erhöhung des Druckes die ´Größe´ der vierdimensionalen Teilchenoszillation verringern.
Ein gefüllter Luftballon in einer Druckkammer wird kleiner, wenn der Druck ansteigt. Der Ballon wird aber größer, wenn ich den Luftdruck in seiner Umgebung verringere. Im Vergleich dazu müßte sich die Teilchenwolke aufblähen, wenn der Impulsgehalt oder die Dichte der Hintergrundstrahlung absinkt ...“
Vasco knurrt vage Zustimmung.
„Das würde aber bedeuten, Vasco, daß es eine Abhängigkeit der Teilchengestalt von den konkreten Umgebungsbedingungen gibt!
Die Teilchenwolken müssen sich den wechselnden Umgebungsbedingungen anpassen und dabei werden sich zwangsläufig auch die subjektiven raum-zeitlichen Maßstäbe, die sie der Bewertung ihrer Umgebung zu Grunde legen, verändern. Und ,“ Paul unterbricht seine Wanderung , „das müssen sie bemerken!“
Vasco nickt kurz mit dem Kopf.
„Du hast mir einmal gesagt, Vasco, daß ein unmittelbar neben einer starken Gravitationsquelle kreisender Körper einer stärkeren Zeitdilatation unterliegt, als ein weit davon entfernter umlaufender Körper.“
Vasco nickt wiederum.
„Wenn ein Teilchen in einem Gravitationsfeld frei fällt,“ setzt Paul zögernd fort, „ dann wird es ständig vom Sog der Gravitationsquelle beschleunigt. Der aus Richtung der Gravitationsquelle anstehende abgeschwächte Impuls wird dabei auf die gesamte Resonanzfigur des Teilchens verteilt. An der Oberfläche eines nahen Teilchens wird deshalb ein geringerer Impulsdruck anstehen, als an der Oberfläche eines entfernten Teilchens. So, wie der Luftballon bei fallendem Luftdruck, müßte also auch ein sich dem Gravitationszentrum näherndes Teilchen größer und größer werden. Im gleichem Maße, wie das Gravitationspotential mit zunehmender Annäherung an das Zentrum wächst, müßten sich die vierdimensionalen Maßstäbe des Teilchens verändern..
Ein direkt zum Zentrum fallendes Elementarteilchen müßte zum Beispiel registrieren, daß die Uhren in den hinter ihm zurückbleibenden Gegenden der Welt schneller und schneller zu gehen scheinen, je näher es dem Attraktor kommt...“
„Diese Form der Zeitdilatation gibt es tatsächlich.“ bestätigt Vasco.
„Schon Mitte des 20. Jahrhunderts hat man die Zeitdilatation im Gravitationspotential nachgewiesen indem man den Gang der Uhren in einem Flugzeug mit dem auf der Erde befindlicher Uhren verglichen hat.
In der Allgemeine Relativitätstheorie bestimmen die Massen die Metrik - und die Metrik bestimmt die Bahnen der Massen. In der Nähe der Massen ist die vierdimensionale Metrik stärker gekrümmt als fern von ihnen. In Gegenden, in denen das Gravitationspotential sehr groß ist gehen die Uhren deshalb langsamer als in Gegenden mit geringem Potential.
Diese Zeitdilatation als Funktion des Gravitationspotential ist aber eine Prognose, die nur Spezialisten aus der Allgemeinen Relativitätstheorie ableiten können. Es gibt weder ein plausibles Bild noch eine andere wissenschaftliche Theorie, welche zu dieser Zeitdilatation führt.
Nur die Allgemeine Relativitätstheorie ist in der Lage die Wirklichkeit in dieser Beziehung korrekt widerzuspiegeln ...“
Vasco nickt anerkennend. „Es ist für mich wirklich erstaunlich, daß du nun aus dem Jonas´ Modell ganz ähnliche Schlussfolgerungen ziehst.
Jonas gelingt damit etwas für unmöglich Gehaltenes: er macht sehr Abstraktes wieder vorstellbar.
Ursprünglich haben mich seine gefüllten Räume, seine Impulsströme und die darin schwebenden Teilchenresonanzen nicht gerade begeistert. Doch dann erkannte ich die Anschaulichkeit seines Weltmodells. Bisher nur mathematisch formulierte Fragen und Paradoxa konnte ich auf einmal in Worte und Bilder fassen. Heute stören mich auch die mit seinem Weltbild verbundenen Hypothesen nicht mehr, Paul.
Wenn man sich dieser Hypothesen bewußt ist, dann sind sie auch keine Gefahr mehr und außerdem,“ Vasco winkt lächelnd ab, „ist ohnehin alles, was wir zu wissen behaupten, im Grunde nur Hypothese...“
E= m c²
„Nun komme ich wohl doch zu spät!“ kommt es plötzlich ärgerlich von hinten. Unmittelbar darauf schließt Eli lautstark die Kabinentür.„Wenn ich Vascos Hypothesen-These richtig verstehe, dann habt ihr das Geschehen in der Welt inzwischen wirklich erschöpfend erklärt.“ seine Ironie ist unverkennbar.
„Davon kann ja nun wirklich noch keine Rede sein. “ entgegnet Paul trocken. „Andererseits nimmt für mich bisher Unvorstellbares tatsächlich langsam Konturen an. Es ist sogar viel einfacher als ich befürchtet habe. Die Trägheit, die Gravitation, kurz gesagt der Raum der Allgemeinen Relativitätstheorie bekommt auf einmal so etwas wie eine Struktur, Eli. Das ´Krumme´ im Vakuum erscheint mit plötzlich vorstellbar.
Andererseits ist das Vakuum nun nicht mehr ganz so leer wie ich das früher vermutet habe. Da dieses Vakuum aber auch erklärt, weshalb es eine Grenzgeschwindigkeit für alle massebehafteten Teilchen gibt ...“
„Dann erkläre mir doch gleich, was hinter der berühmten Gleichung, E = m * c² steckt? “ unterbricht Eli die drohende Schwärmerei.
„So schwierig ist das gar nicht.“ antwortet Paul gelassen. „Bei Jonas sind Elementarteilchen Resonanzzustände zwischen einem oder wenigen oszillierenden Urobjekten und unendlich vielen freien Urobjekten der Hintergrundstrahlung.
Die Oszillationsfigur der Teilchen orientiert sich dabei immer an der lokal herrschenden Hintergrundstrahlung. Ob sich das Teilchen nun dazu bewegt oder ob es ruht: jedes Teilchen fühlt sich subjektiv immer in Ruhe. Die Teilchen bewegen sich also nicht im klassischen Sinne ´durch ein Medium hindurch´, sondern sie pflanzen sich darin reibungslos fort.“
Eli trifft ein kurzer Blick.
„In Einsteins Gleichung sind Masse und Energie über den Faktor Lichtgeschwindigkeit miteinander verbunden. Diese Erkenntnis verblüffte wohl schon damals die Menschen und auch ich habe das bisher nur ´zur Kenntnis´ genommen. Aber ich habe ihn, ehrlich gesagt, niemals ´verstanden´.
Eli nickt eifrig.
"E=m*c², oder E/c² =m - es macht keinen Unterschied, Eli, ich konnte die Gleichung drehen und wenden wie ich wollte, mir war das in ihr steckende Bild immer gleich rätselhaft.
Im Modell von Jonas aber wird der Zusammenhang zwischen Masse und Energie plötzlich klar. Ja, er liegt förmlich auf der Hand. Die im Jonas´ Raum befindlichen Teilchenwolken bestehen schließlich aus impulsstarken und deshalb unerhört schnell in einer Oszillationsfigur hin- und her rasenden Urobjekten. Sie sind regelrechte Verkörperungen von eingesperrtem Impuls - von Energie.
Will man die Bewegung eines Teilchens vor dem Hintergrund verändern, so kann man das Teilchen ´von außen´ anstoßen - ihm einen Impuls vermitteln.
Im Ergebnis wird das Teilchen von seiner bisherigen Bahn abweichen. Nach dem Stoß steckt der vermittelte Impuls im Teilchen. Die Größe der durch den Impuls vermittelten Bahnabweichung steht im Verhältnis zur Masse des Teilchens, man sagt auch dazu ´Trägheit´. Eine Eigenschaft der Masse ist schließlich Trägheit , ist der Widerstand, mit dem sich das schwere Teilchen einer Veränderung seines ´natürlichen´ Bewegungszustand zu widersetzen scheint.
Eine bestimmte Masse entspricht also einer bestimmten Menge an Impuls. Und diese wiederum entspricht einer bestimmten Menge Energie.
Somit ist der Zusammenhang zwischen der Masse eines Teilchens und der in ihm eingesperrten Energie gegeben. Masse und Energie sind einander proportional.
Doch das ist noch nicht alles, Eli: Jonas´ Materievorstellung veranschaulicht auch den Zusammenhang zwischen dem Gesamtimpuls einer Teilchenoszillion und deren Bewegungszustand vor dem Hintergrund. Wenn ein Teilchen zum Beispiel sehr schnell.."
„Nun wird mir manches klar,“ Eli unterbricht Paul, „Vasco hat gestern abend diesen Artikel gegeben. Ich habe diesen Teil nicht verstanden.
Jonas´Bild suggeriert, dass sich die Gesamtenergie eines Teilchens aus seiner Ruheenergie - der Ruhemasse - und der ehemals hineingepumpten Bewegungsenergie, dem relativistischen Anteil, zusammensetzt. Ein energiereiches, weil sich schnell bewegendes Elementarteilchen ist deshalb schwerer. Dann müsste aber auch ein schwereres Elementarteilchen mehr Raum ´in Anspruch nehmen´, als ein ruhendes, doch, ..." Eli wiegt zweifelnd den Kopf, „ diese Kalkulation geht zwar in manchen Fällen auf, doch am Ende sehe ich da einige eklatante Problem auf uns zukommen, Paul.“ Eli grinst säuerlich.
„Wenn du zum Beispiel das Volumen eines Stoffes im kalten und im warmen Zustand miteinander vergleichst, dann wird der warme Stoff tatsächlich mehr Raum einnehmen. In diesem Fall wäre der Zusammenhang zwischen Energie, Masse und Inanspruchnahme von Raum zutreffend, aber, " Eli zwinkert nervös mit den Augen, „selbst ein Biologe weiß, daß ein Proton ca. 60 000 mal schwerer als ein Elektron ist, aber trotzdem ist es unvergleichlich viel kleiner als dieses. Obwohl es also kleiner ist, also extrem weniger Raum in Anspruch nimmt, steckt viel, sogar sehr viel mehr Energie in ihm drin !“
„Proton und Elektron haben ein Masseverhältnis von 1 : 60 000,“ wiederholt Paul langsam. „Er denkt ein paar Sekunden nach , dann schüttelt er gelassen den Kopf. „Das sind doch ganz verschiedene Teilchen, Eli. Sie haben also auch ganz verschiedene Schwingungsgestalten. Und verschiedene Schwingungsfiguren werden ihr Inneres auch verschieden stark vor dem Hintergrund abschirmen und dann, ..."
„Ich verstehe,“ murmelt Eli und schaut an die Decke. „Du meinst, die Oszillationswolken werden unterschiedlich ´dicht´ sein. Hmmm! Da ein Proton sowohl klein als auch schwer ist, müsste es in einer kleinen, dafür aber extrem dichten und kompakten Wolke oszillieren. Dagegen müsste ein Elektron dann eine wattig große Wolke sein. Das klingt gar nicht dumm.“
Vasco war dem Gespräch zwischen Paul und Eli mit wachsender Ungeduld gefolgt. „Dieses Thema ist auch sehr interessant, Eli,“ unterbricht er die beiden und wuchtet sich energisch aus dem Sessel, „doch selbst für die einfachsten Aspekte der elektromagnetischen Wechselwirkung brauchen wir viel, sehr viel mehr Zeit, als mir heute noch zur Verfügung steht. Ich muss nämlich schnellstens in die Navi. Der," mit dem Finger zeigt er auf den Biologen, „weiß Bescheid, Paul. Er hat mit Sylvia gesprochen und er weiß auch worauf es morgen ankommt. Die Invarianz wird ganz bestimmt ein Thema .“
Eli nickt gehorsam und winkt Paul. „Gehen wir". Paul ist von diesem plötzlichen Aufbruch natürlich überrascht, doch nach einem Blick auf die Uhr wird ihm einiges klar.
Auf dem Gang vor Vascos Kabine begegnet ihnen Nilsson. Wie immer trägt er einen abgeschabten, alten Aktenkoffer in der Hand.
´Old´ Nilsson - wie er gelegentlich genannt wird, - ist für die Antriebe der Heidelberg zuständig. Ein typischer Quantenphysiker, hat Mary einmal zu gesagt. Paul hatte bisher nur wenig mit ihm zu tun. Um so mehr überrascht ihn , das Nilsson im Gang spontan die Richtung wechselt und auf sie beide zusteuert.
„Hallo, Eli. High Paul!“ begrüßt er sie mit leicht näselnder Stimme. „Wolltet ihr bei Vasco nachsehen ob die Katze tot ist?
Oder habt ihr inzwischen die Kausalität hinter der Schrödingergleichung entdeckt?“
Ohne eine Antwort abzuwarten macht er nun kehrt und tappt leise kichernd mit seinem Koffer davon.
Paul schaut ihm verdattert hinterher. "Katze tot?" wiederholt er tonlos und schaut Eli groß an. "Sind unsere Katzen in Schwierigkeiten geraten?"
"Nilsson spricht oft in Rätseln," kichert Eli und winkt ab. Ich glaube, Nilsson meinte ´Schrödingers Katze´. Er war gestern auch bei Vasco. Und ich bin sicher, Vasco hat die Gelegenheit genutzt und den Quantenmechaniker mit dem Jonasmanuskript gelöchert." Und damit war für Eli die Episode abgehakt.
Auf die Frage „Warum fällt
ein Stein, den wir emporheben und darauf loslassen, zur Erde?“
antwortet man gewöhnlich: „Weil er von der Erde angezogen wird.“
Die moderne Physik formuliert die Antwort etwas anders aus
folgendem Grunde. Durch genaueres Studium der elektromagnetischen
Erscheinungen ist man zu der Erkenntnis gekommen, daß es eine
unvermittelte Wirkung in die Ferne nicht gebe. Zieht zum Beispiel ein
Magnet ein Stück Eisen an, so darf man sich nicht mit der Auffassung
zufrieden geben, daß der Magnet durch den leeren Zwischenraum
hindurch auf das Eisen direkt einwirke, sondern man stellt sich nach
Faraday vor, daß der Magnet in den ihn umgebenden Raum etwas
physikalisch reales stets hervorrufe, was man als magnetisches Feld
bezeichnet. Dies magnetische Feld wirkt einerseits wieder auf das
Eisenstück ein, so daß es sich zum Magneten zu bewegen strebt. Die
Berechtigung dieses an sich willkürlichen Zwischenbegriffes wollen
wir hier nicht erörtern. Es sei nur bemerkt, daß man mit seiner
Hilfe die elektromagnetischen Erscheinungen, insbesondere die
Ausbreitung der elektromagnetischen Wellen, viel befriedigender
theoretisch darstellen kann, als ohne denselben. Analog faßt man
auch die Wirkung der Gravitation auf.
A
Einstein in /14/ § 16 Das Gravitationsfeld
Wissenschaft - nicht nur die Physik- arbeitet meines Erachtens immer mit Modellen der Wirklichkeit. Sofern die daraus abgeleiteten Theorien gute Prognosen ermöglichen, bezeichnen wir die Theorie als richtig. Treten Differenzen zwischen der Prognose aus der Theorie und der Beobachtung auf, wird die Theorie in Frage gestellt. Theorien werden unablässig ergänzt, präzisiert und manchmal auch von neueren Theorien ersetzt, welche die Beobachtungen besser erklären können.
Doch auch diesen Neuen liegt immer wieder ein Modell zu Grunde. Das wird so bleiben. Ein vollständiges Abbild der Wirklichkeit, ein Modell oder gar eine Theorie ´von Allem´, die wird es nie geben, wie auch den Dämon .